
中国において、度量衡(長さ・容積・重さ)は、周代(紀元前11世紀~紀元前221年)後期に整備され、後の秦代(紀元前221年~紀元前206年)に、全国的に統一された度量衡が制定されとされます。
その内の「度(容積)」の標準器とされたものが、「嘉量(カリョウ)」と呼ばれます。
【周禮:冬官考工記*1】に、その基準が記されています。
栗氏為量。改煎金錫則不耗,不耗然後權之,權之然後準之,準之然後量之。量之以為釜,深尺,內方尺而圜其外,其實一釜。其臀一寸,其實一豆;其耳三寸,其實一升。重一鈞。其聲中黃鐘之宮。概而不稅。其銘曰:「時文思索,允臻其極。嘉量既成,以觀四國。永啟厥後,茲器維則。」凡鑄金之狀:金與錫黑濁之氣竭,黃白次之;黃白之氣竭,青白次之;青白之氣竭,青氣次之。然後可鑄也。
後の西漢代
(紀元前202年頃~8年頃、日本では「前漢」とも呼ばれます)後期から東漢代
(25年~220年、日本では「後漢」とも呼ばれます)にかけて、新
(シン、8年~23年)の皇帝となった王莽
(オウモウ、紀元前46年~23年)は、改めて度量衡を見直し、それに合わせて標準器を作り直します。
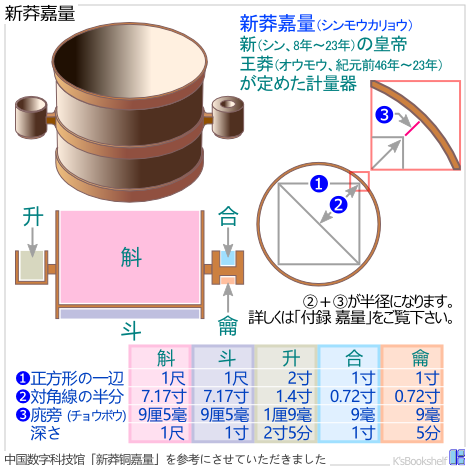
これが「新莽嘉量
(シンモウカリョウ)」と呼ばれ、大変精度の高い標準器でした。
(ちなみに、日本の歴史でいえば、弥生時代中期に当たります。)
二千年も前に作られた器の、以下、その「正確さ」を検証してみたいと思います。
「新莽嘉量(シンモウカリョウ)」の精度を検証する前に、漢代(紀元前202年頃~220年)の度量衡(長さ・容積・重さ)を知っておくことが必要になります。
「度(長さ)」については、【漢書:志:律曆志:律曆志上*1】に、その基準が記されています。
度者,分、寸、尺、丈、引也,所以度長短也。本起黃鐘之長。以子穀秬黍中者,一黍之廣,度之九十分,黃鐘之長。一為一分,十分為寸,十寸為尺,十尺為丈,十丈為引,而五度審矣。其法用銅,高一寸,廣二寸,長一丈,而分寸尺丈存焉。
とあり、要約すれば、
- 度(長さ)には分・寸・尺・丈・引の五つの単位を用いる(度者,分、寸、尺、丈、引也)
- 黃鐘の長さを基準とする(本起黃鐘之長)
- 黃鐘の長さは、キビ(黍)・クロキビ(黒黍)の実の中粒(標準的な大きさの粒)の幅の九十個分の長さである(以子穀秬黍中者,一黍之廣,度之九十分,黃鐘之長)
- (この黃鐘の長さの基準となっているキビ(黍)・クロキビ(黒黍)の実の)一粒の幅を一分(一為一分)
- 十分が一寸(十分為寸)
- 十寸が一尺(十寸為尺)
- 十尺が一丈(十尺為丈)
- 十丈が一引(十丈為引)
- とし、五つの単位の関係を明確にする(而五度審矣)
- 測定器(物差し)は銅製とし(其法用銅)
- 厚みは一寸、幅は二寸、長さは一丈とする(高一寸,廣二寸,長一丈)
- これによって、分・寸・尺・丈が測定できる(而分寸尺丈存焉)(この物差しでは、「分」は測定できないと思われますが)
ということになります。
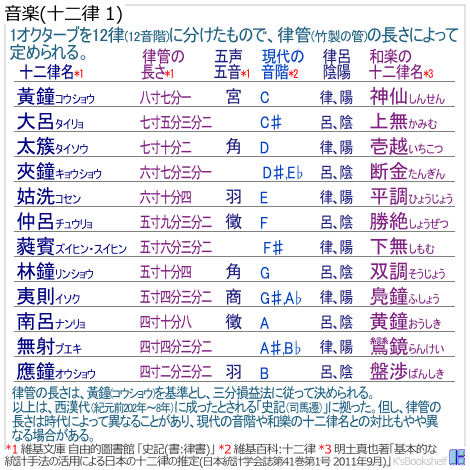
ここで「黃鐘(コウショウ)」とは、12階の音の高さ(十二律、ジュウニリツ)」の第一音をいいます。(「十二律図」参考)
度量衡に、直接の関係はありませんが、参考までに【史記:書:卷二十五:律書*2】の一部を引きます。
律數:(中略)黃鐘長八寸七分一,宮。大呂長七寸五分三分一。太蔟長七寸七分二角。夾鐘長六寸一分三分一。姑洗長六寸七分四羽。仲呂長五寸九分三分二徵。蕤賓長五寸六分三分一。林鐘長五寸七分四角。夷則長五寸四分三分二商。南呂長四寸七十分八徵。無射長四寸四分三分二。應鐘長四寸二分三分二羽。
ちなみに、十二律のうち、第一音~第十一音の奇数音を六律(ロクリツ)、第二音~第十二音の偶数音を六呂(リクロ)といい、合わせて律呂(リツリョ)、また呂律(リョリツ、ろれつ)といいます。
「呂律が回らない」は、「音の調子が合わない」の意で、これを引いて「言いようの抑揚・強弱が合わない、言っていることがよく分からない」の意に用いられます。酔った時の口調などを指します。
「度」「量」をメートル法で表した場合の値については、資料が見つからず、維基百科の「中國度量衡」を参考にさせていただきました。*3
漢代(紀元前202年~220年)の「度」「量」をメートル法で表すと、以下のようになります。
秦代(紀元前221年頃~紀元前207年頃)も、ほぼ同じです。
(参考までに「衡」も示しました)
| 度(長さ) | 1引=10丈=2310cm, 1丈=10尺=231cm, 1尺=10寸=23.1cm, 1寸=10分=2.31cm, 1分=0.231cm |
| 量(容積) | 1斛=10斗=20000mL, 1斗=10升=2000mL, 1升=10合=200mL, 1合=2龠=20mL, 1龠=5撮=10mL, 1撮=4圭=2mL, 1圭=0.5mL |
| 衡(重さ):秦 | 1石=4鈞=30360g, 1鈞=30斤=7590g, 1斤=16兩=253g, 1兩=24銖=15.8g, 1銖=0.66g |
| 衡(重さ):西漢 | 1石=4鈞=29760g, 1鈞=30斤=7440g, 1斤=16兩=248g, 1兩=24銖=15.5g, 1銖=0.65g |
| 衡(重さ):東漢 | 1石=4鈞=26400g, 1鈞=30斤=6600g, 1斤=16兩=220g, 1兩=24銖=13.8g, 1銖=0.57g |
これ以降、検証のために計算式や計算結果を示しますが、特に断りがない限り、上の数値・単位を使います。
当時の度量衡が分かったところで、これから新莽嘉量の話になりますが、
まず、その形について、再び【漢書:志:律曆志:律曆志上*1】を引きます。
其法用銅,方尺而圜其外,旁有庣焉。其上為斛,其下為斗。左耳為升,右耳為合龠。其狀似爵,以縻爵祿。上三下二,參天兩地,圜而函方,左一右二,陰陽之象也。其圜象規,其重二鈞,備氣物之數,合萬有一千五百二十。聲中黃鐘,始於黃鐘而反覆焉,君制器之象也。
とあり、要約すれば、
- 測定器は銅製とし(其法用銅)
- (底面は)一辺一尺の正方形が内接する円とし(方尺而圜其外)
- (既定の容量に合わせるために)足りない分を広げる(旁有庣焉)
- 上の枡を斛(其上為斛)(1斛=10斗=20000mL)
- 下の枡を斗(其下為斗)(1斗=10升=2000mL)
- 左に取り付けた枡を升(左耳為升)(1升=10合=200mL)
- 右に取り付けた枡は(上を)合(下を)龠とする(右耳為合龠)(1合=2龠=20mL、1龠=5撮=10mL)
- (以降略)
ということになります。
実物は、國立故宮博物院のページで見ることができます。
國立故宮博物院のページ右上の検索ボタンから、「嘉量」などのキーワードで検索して下さい。
(日本語のページもありますので、是非一度ご覧になることをお進めします)
余談ですが、嘉量について調べようと思い立ったのは、「庣」の意味を調べている時でした。
(興味のない方は、読み飛ばして、次の「新莽嘉量の寸法」へどうぞ。)
【廣韻:下平聲:蕭:祧:庣】に、
不滿之皃
とあり、「満たないさま」「足りないさま」の意ですが、更に、【說文解字注】に、
其篆書字題斛旁云:律嘉量斛,方一尺而圜其外,庣旁九犛五豪,冪一百六十二寸,深一尺,積一千六百二十寸,容十斗。
とあり、一挙に分からなくなりました。
「其篆書字題」や「方一尺而圜其外」の「外」が分からず、ネットで「嘉量」を調べている時に、
中国数字科技館の「器具名称:新莽铜嘉量1」のページに辿り着き、
「其篆書字題」は「新莽嘉量の銘文」、
「方一尺而圜其外」は「一辺一尺の正方形が内接する円」、
「庣旁九犛五豪」は「(既定の容量に合わせるために)足りない分として九犛五豪広げる」
の意であることが、やっと分かりました。
中国数字科技館には、本当に感謝しています。
実は、そのページに、新莽嘉量の銘文を基に、容量を計算・検証している部分があり、これに興味を持ったことが発端でした。
余談が長くなってしまいました。
次に、その寸法ですが、新莽嘉量には、以下のような銘文があるそうです。*1
律嘉量斛,方尺而圜其外,庣旁九厘五毫,冥百六十二寸,深尺,積千六百二十寸,容十斗。
律嘉量斗,方尺而圜其外,庣旁九厘五毫,冥百六十二寸,深寸,積百六十二寸,容十升。
律嘉量升,方二寸而圜其外,庣旁一厘九毫,冥六百四十八分,深二寸五分,積万六千二百分,容十合。
律嘉量合,方寸而圜其外,庣旁九毫,冥六十二分,深寸,積千六百二十分,容二籥。
律嘉量籥,方寸而圜其外,庣旁九毫,冥六十二分,深五分,積八百一十分,容如黄钟。
引用させていただいた中国数字科技館のページは、簡体字であるため、ここでは「积」は「積」に変えてあります。
また、「合」「籥」の「冥六十二分」は「冥百六十二分」の誤りと思われます。
「斛」を例にとれば、
- 斛の規格は、一辺一尺の正方形が内接する円で(律嘉量斛,方尺而圜其外)
- (既定の容量に合わせるために足りない分として)九厘五毫広げる(庣旁九厘五毫)
(従って、この正方形の対角線の長さの半分+庣旁チョウボウ=半径、となります)
- その面積は百六十二寸(冥百六十二寸)
- 深さは一尺(深尺)
- 体積は千六百二十寸(積千六百二十寸)
- 容積は十斗(容十斗)
ということになります。
「冥(冪)」は冪乗(ベキジョウ)の意で面積、「積」は体積のことで、「冥百六十二寸」の「寸」は「寸2」、「積千六百二十寸」の「寸」は「寸3」ということになります。
従って、メートル法に変換すれば、1寸=2.31cmとし、「冥(面積)」「積(体積)」は、それぞれ以下のようになります。
冥1寸=(2.31cm)2=5.3361cm2
積1寸=(2.31cm)3=12.326391cm3
「斛」を例にとれば、
冥百六十二寸(162)×冥1寸(5.3361cm2)=864.4482cm2
積千六百二十寸(1620)×積1寸(12.326391cm3)=19968.75342cm3
になります。
これで、漢代(紀元前202年~220年)の度量衡が分かり、新莽嘉量の寸法も分かり、いよいよ、底面の面積・容積の計算ができることになります。
*1 中国数字科技館:器具名称:新莽铜嘉量1
國立故宮博物院:新銅嘉量的剖面圖及本院檢校的結果
以下は、「新莽嘉量の寸法」に示した新莽嘉量にある銘文*1の数値を基に、「漢代の度量衡」に示した数値を使って、新莽嘉量の容積を計算した結果です。
①正方形の一辺の長さ(単位寸、1尺=10寸、1寸=10分)
②正方形の対角線の長さの半分(単位寸)=(①正方形の一辺の長さ×√2)/2
③庣旁(チョウボウ、既定の容量に合わせるために足りない分として広げる長さ、単位寸、1寸=10分、1分=10厘、1厘=10毫)
④正方形が内接する円の半径(単位寸)=②正方形の対角線の長さの半分+③庣旁
⑤底面の面積(単位寸
2)=④半径×④半径×円周率(3.1416)
⑥深さ(単位寸、1尺=10寸、1寸=10分)
⑦容積(単位寸
3)=⑤底面の面積×⑥深さ
⑧容積(単位cm
3=mL)=⑦容積(寸)×1寸(2.31cm)
3
⑨漢代の量(容積、単位mL)
⑩漢代の量(容積)と計算上の容積との差(単位%)=(⑧容積-⑨漢代の量)/⑨漢代の量
但し、1寸=2.31cm、円周率(π)=3.1416
| ①
寸 | ②
寸 | ③
寸 | ④
寸 | ⑤
寸2 | ⑥
寸 | ⑦
寸3 | ⑧
cm3=mL | ⑨
mL | ⑩
% |
| 斛 | ①方尺而圜其外,③庣旁九厘五毫,⑤冥百六十二寸,⑥深尺,⑦積千六百二十寸 |
| 10.0 | 7.071 | 0.095 | 7.166 | 161.329 | 10.0 | 1613.291 | 19886.056 | 20000 | -0.570% |
| 斗 | ①方尺而圜其外,③庣旁九厘五毫,⑤冥百六十二寸,⑥深寸,⑦積百六十二寸 |
| 10.0 | 7.071 | 0.095 | 7.166 | 161.329 | 1.0 | 161.329 | 1988.606 | 2000 | -0.570% |
| 升 | ①方二寸而圜其外,③庣旁一厘九毫,⑤冥六百四十八分,⑥深二寸五分,⑦積万六千二百分 |
| 2.0 | 1.414 | 0.019 | 1.433 | 6.453 | 2.5 | 16.133 | 198.861 | 200 | -0.570% |
| 合 | ①方寸而圜其外,③庣旁九毫,⑤冥六十二分,⑥深寸,⑦積千六百二十分 |
| 1.0 | 0.707 | 0.009 | 0.716 | 1.611 | 1.0 | 1.611 | 19.858 | 20 | -0.708% |
| 籥 | ①方寸而圜其外,③庣旁九毫,⑤冥六十二分,⑥深五分,⑦積八百一十分 |
| 1.0 | 0.707 | 0.009 | 0.716 | 1.611 | 0.5 | 0.806 | 9.929 | 10 | -0.708% |
「合」「籥」の「冥六十二分」は「冥百六十二分」の誤りと思われます。
いずれも、差は1%未満でした。
1寸=2.31cm としたことや、円周率(π)=3.1416 としたことなど、当時とは多少の差があるでしょうから、1%未満の差は、無視できる程度のものと考えられます。
*1 中国数字科技館:器具名称:新莽铜嘉量1
國家度量衡標準實驗室:
新莽嘉量
学術雑誌論文:新莽嘉量について 岩田重雄著
当時は、円周率をどのような値と考えていたのでしょうか?
「新莽嘉量の寸法」に示した新莽嘉量にある銘文*1の数値を基に考えてみます。
「斛」を例にとれば、「方尺而圜其外,庣旁九厘五毫,冥百六十二寸」とあり、一辺一尺の正方形が内接する円の半径に九厘五毫を加えた大きさの底面(半径は上の「新莽嘉量の精度」の表の④ 7.166寸)の面積は162寸2(冥百六十二寸)です。
ということは、
円周率(π)=面積/(半径×半径)=162寸2/(7.166寸×7.166寸)=3.15472427
となります。
同様に、円周率(π)を逆算してみると、「升」では 3.155604924、「合」「籥」では 3.160013732になります。
それでは、「斛」「升」「合」「籥」の平均値3.157を円周率(π)として、上の表を作り変えてみると、
| ⑧
cm3=mL | ⑨
mL | ⑩
% |
| 斛 | 19983.158 | 20000 | -0.084% |
| 斗 | 1997.088 | 2000 | -0.084% |
| 升 | 199.709 | 200 | -0.112% |
| 合 | 19.943 | 20 | -0.251% |
| 籥 | 9.972 | 10 | -0.251% |
となります。
見事なほどの正確さですね。
二千年も前の、設計技術や、それを形にする工作技術の水準の高さには、驚かされます。
*1 中国数字科技館:器具名称:新莽铜嘉量1
新莽嘉量が、大変精度の高い計量器であったことは分かりましたが、疑問に思ったことがありました。
以下、新莽嘉量にある銘文*1の「斛」を例にとると、
律嘉量斛,方尺而圜其外,庣旁九厘五毫,冥百六十二寸,深尺,積千六百二十寸,容十斗。
「深さが一尺
(深尺)、一辺一尺の正方形が内接する円
(方尺而圜其外)を九厘五毫広げた
(庣旁九厘五毫)円を底面とする円柱の容器の容量を一斛とし、一斛は十斗に等しい」とあります。
深さが一尺で、一辺一尺の正方形が内接する円の場合の円柱の体積は、19362.295cm
3 で、1斛=10斗=20000cm
3 に少し足りません。
そこで、底面の大きさを九厘五毫広げることにしたのですが、どうして、単に「深さを一尺とし、半径を七寸一分六厘六毫とする円柱」とはしなかったのでしょうか?
(冥百六十二寸にするには、底面の半径を七寸一分六厘六毫、直径を一尺四寸三分三厘一毫にする必要があります)
数学や物理学では、原理を解きまた説く際に、「より簡潔に」「より美しく」、という考え方をするそうです。
よく例に挙げられるのは、アインシュタインによる
E=mc^2 (エネルギー=質量×光速の2乗)
という式です。
非常に難解な概念ですが、それを表す計算式は、簡潔ですね。
元に戻りますが、当時の数学者も、同じ考えだったのではないでしょうか?
「斛」を例にとれば、幾つもの単位や数値を用いることなく、ただ「一尺」だけを基準として、量を定義しようとしたのではないか、と考えています。
そのために、「底面は一辺一尺の正方形が内接する円に足りない分として九厘五毫広げる、深さは一尺」とした、のではないかと思っています。
「底面の円の直径を一尺四寸三分三厘一毫、深さを一尺」とする定義よりも、確かに「美しい」と思います。
*1 中国数字科技館:器具名称:新莽铜嘉量1














